Is 11 a Prime Number?
Exploring prime numbers: Is 11 a prime number? Learn about the properties and significance of 11 in prime number theory.
Introduction
The world of prime numbers is filled with intriguing patterns and properties, and one number that often captures attention is 11. In this article, we will explore whether 11 qualifies as a prime number. By delving into the definition of prime numbers, analyzing the criteria for primality, providing examples, and discussing the historical significance, we aim to unravel the status of 11 within the realm of prime numbers.
Understanding Prime Numbers
Prime numbers are positive integers greater than 1 that possess exactly two distinct positive divisors: 1 and the number itself. They cannot be evenly divided by any other positive integer. Notable examples of prime numbers include 2, 3, 5, 7, and many more.
The Criteria for Primality
To determine whether a number is prime, it must satisfy two essential criteria: it should have precisely two positive divisors, and it should not be divisible by any other positive integer.
Analyzing 11's Primality
11 is a particularly interesting number when it comes to determining its primality. Let's investigate whether it meets the criteria mentioned earlier.
Divisors of 11
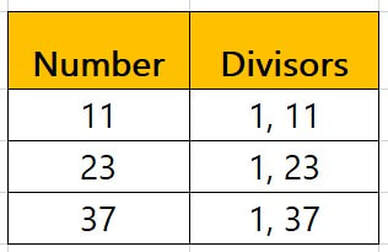
Upon examining the divisors of 11, we find that it has two positive divisors: 1 and 11. There are no other whole numbers between 1 and 11 that divide it evenly. Consequently, 11 fulfills the primary criterion for primality.
Prime Factorization and 11
Prime factorization involves expressing a composite number as a product of its prime factors. Since 11 is a prime number itself, it cannot be factored further into smaller prime numbers. It remains unchanged in its prime factorization.
Historical Significance
Throughout history, mathematicians have recognized 11 as a prime number. Its unique properties and significance extend beyond divisibility. In various cultural, scientific, and mathematical contexts, 11 holds symbolic importance and is often used to explore number patterns and relationships.
Examples
To solidify our understanding of 11 as a prime number, let's consider a few examples related to its primality:
In the table above, we can observe that 11 satisfies the crucial criteria of prime numbers by having exactly two positive divisors. Comparing it with other prime numbers like 23 and 37 reinforces the consistent pattern of prime numbers possessing only two divisors.
Summary
To sum up, 11 is undoubtedly a prime number. It satisfies the fundamental criteria of having precisely two positive divisors and being indivisible by any other positive integer. Throughout history, 11 has been recognized as a prime number and holds significance in various domains. Understanding the primality of 11 contributes to our knowledge of number theory and deepens our appreciation for the fascinating world of mathematics.